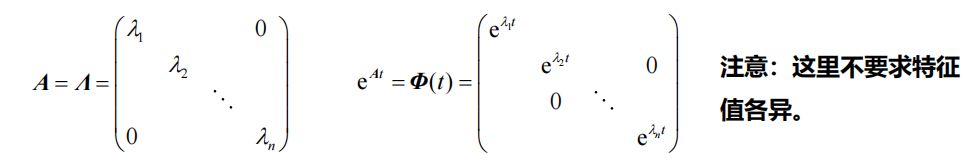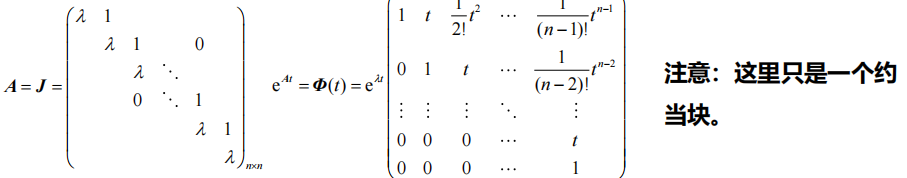现代控制理论

状态空间基础

状态空间基本概念

• 状态：动力学系统的状态定义为信息的集合

  注意点：动力学系统在的状态是由的状态和后的输入唯一确定的，与前的状态和输入无关

• 状态变量：能完全表征系统运动状态的最小一组变量，选取不唯一

• 状态向量：状态变量组成的向量

• 状态空间：由状态向量张成的向量空间

• 状态空间表达式：状态方程和输出方程组合

• 状态维度：完全表征动力系统动态行为状态的最小数目

  注意点：与自由度不相等

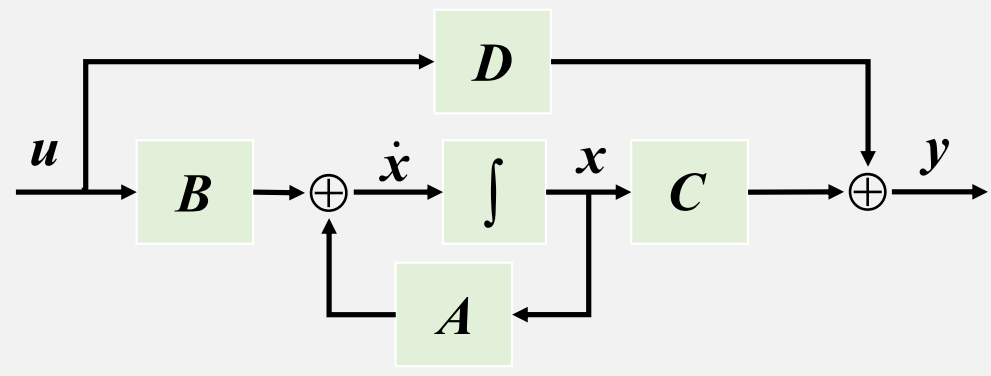
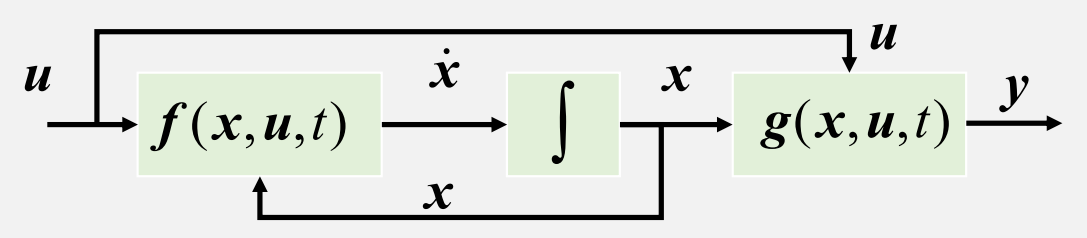
状态空间的一般形式

单输入单输出,多输入多输出

线性系统：

系统矩阵，控制矩阵，输出矩阵，直接传递矩阵

非线性系统：

离散系统：

非线性形式

线性形式

状态空间表达式的建立

传递函数建立状态空间表达式

传递函数：

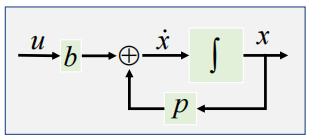
直接分解法

**，惯性系统**

选取中间传递函数：

写为微分方程形式

状态空间表达式

这个形式叫能控标准型

**，非惯性系统**

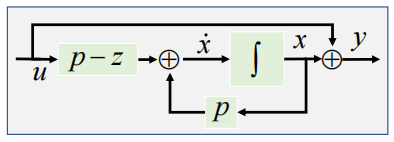
传递函数降价 选取中间传递函数：

状态空间表达式

串联分解

**，惯性系统**

传递函数整理

传递函数实现

• 基本环节1
• 基本环节2

系统逻辑框图

第一种分解方式

第二种分解方式

并联分解

**以只有一个r阶重根为例**

传递函数整理

中间变量选取

状态空间表达式

状态空间表达式的坐标转换

状态可逆线性变换（坐标系切换）

转换矩阵

坐标转换 矩阵转换关系

状态空间表达式与传递矩阵的关系

注意点：状态可逆线性变换（坐标系切换）不影响传递函数

线性定常系统状态方程的解

齐次状态方程的解

纯量微分方程的解

纯量方程： 设方程的解为： 代入原式，并且对任意都满足，所以：

所以最终解为：

齐次向量微分方程： 同理可得： 记作:

这里也可以用拉氏变换法求解

取拉氏变换得： 可得： 假设: 可验证： 假设成立，所以拉氏变换

最终结果跟前文相同

我们记,称为状态转移矩阵

当从开始状态转移，我们可记作

对于状态转移矩阵，它有以下性质：

• 是微分方程的唯一解

状态转移矩阵的计算

直接计算

• 对角线

  

• 约当标准型

  

特征分解

Laplace变换

非齐次状态方程的解

非齐次向量微分方程： 解的： 其中称作零输入解，称为零状态解

零状态解的计算

Laplace变换

线性系统的可控性和可观测性

数学准备知识

凯莱-哈密尔顿(Cayley-Hamilton)定理

记系统矩阵的特征多项式为，则矩阵满足：