轨道力学及应用第三节课

KEPLER轨道与轨道要素

限制性二体问题基本解

Kepler轨道的三个常量

轨道角动量常矢量（位置矢量叉积）

表明解矢量恒在一个平面内，称为Kepler轨道平面

轨道能量常量（速度点积）

Laplace常矢量（角动量矢量叉积）

和刚好构成天文坐标系中的一组极点和基准点，构成所谓的拱线坐标系

Kepler轨道常量之间的约束关系

• 垂直约束关系

• 幅值约束关系

Kepler轨道常量（2个常矢量，1个常标量） 一共7个变量，同时满足2个约束条件，还有5个独立变量，表明轨道位置速度矢量确定的三个轨道常量就可确定5个独立变量； 限制二体运动方程运动方程共有6个积分常量，而5个参数可以由Kepler轨道常量确定，表明仍有1个微分方程未解，对应最后1个积分常量； Kepler轨道最终可由1个微分方程描述（真近点角与时间关系）

Kepler轨道方程（轨道位置的关系）

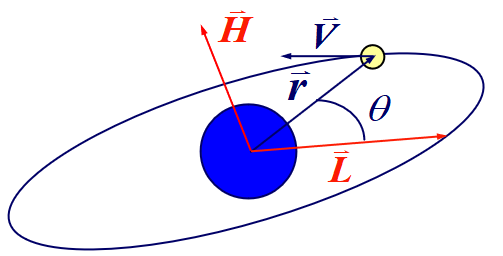
真近点角：和之间的夹角

半通径：

偏心率：

Kepler轨道平面内轨道速度关系

其中称作轨道速度倾角

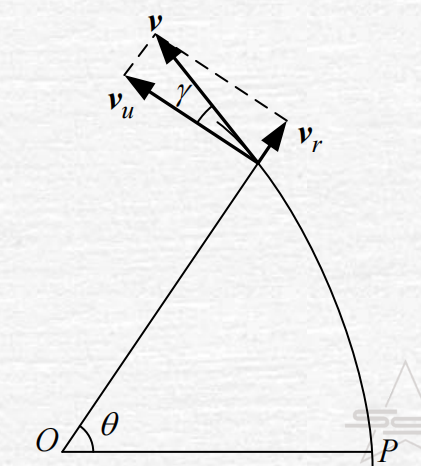
轨道前向速度： 轨道径向速度：

Kepler轨道一般特性

椭圆轨道

近地点、远地点、长半轴与半通径

近地点，远地点 可得 轨道半长轴：

近地点和远地点的轨道速度

可得

椭圆轨道长半轴与Kepler轨道能量

Kepler轨道半长轴的一般性定义

定义半长轴：

逃逸速度

无穷远速度

第一、第二、第三宇宙速度

• 第一宇宙速度：地球半径处环绕地球的轨道速度
• 第二宇宙速度：地球半径处逃逸地球的逃逸速度
• 第三宇宙速度：逃逸地球之后无穷远速度为逃逸太阳引力的轨道速度减去地球公转速度