视觉SALM第二节课

三维空间刚体运动

点、向量和坐标系

空间的一组基，任意向量表示为： 的坐标即

反对称矩阵

坐标间欧式变换

欧式变换：通过旋转和平移进行变换

向量在两坐标中表示： 可得关系： 称为旋转矩阵，因为又是基向量间夹角余弦值，又称方向余弦矩阵

定义n维旋转矩阵的集合： 其中为人为定义，当称为瑕旋转，为一次旋转加一次反射

是特殊正交群的意思

最终欧拉变换关系为：

变换矩阵与齐次坐标

欧式变换： 重新表示为： 其中三维向量添加1称为齐次坐标，将关系变为线性关系，其中称为变换矩阵

优点：使用齐次坐标，多次欧式变换将会有优良形式与线性关系

这种矩阵称为特殊欧式群： 的逆表示一个反向变换：

旋转向量和欧拉角

旋转向量

一个三维向量，指向旋转轴，长度等于旋转角，称为旋转向量，表示为

罗德里格斯公式给出旋转向量到旋转矩阵的变换： 也有旋转矩阵到旋转向量的变换：

欧拉角

缺点：万向锁问题，可论证只要用三个实数表达三维旋转，都不可避免碰到奇异性问题

四元数

我们找不到不带奇异性的三维向量描述方式。四元数既是紧凑的，也没有奇异性

四元数有如下形式： 三个虚部满足以下关系式： 四元数可以表示为一个标量和一个向量：

四元数表示旋转

将三维空间点用四元数表示： 设旋转后变为，由单位四元数指定旋转，则描述为：

四元数到其他旋转表示转换

四元数到旋转矩阵： 四元数到旋转向量：

其他变换

• 相似变换

  三维相似变换的集合称作相似变换群，记作

• 仿射变换

  可逆，但不正交

• 射影变换

  缩放

李群与李代数

李群

集合，计算 ,群记作，且群要求这个运算满足以下条件：

李群：具有连续（光滑）性质的群

李代数

李代数的引出

随着时间变化，为时间函数,有： 求导整理有： 于是存在一个，满足： 所以有： 在附近，保持为常数

于是上述式子看作解纯量微分方程且，可以得到： 时，,有：

李代数的定义

集合,数域，二元运算，李代数记作,满足以下性质：

其中二元运算称作李括号

李代数

对应的李代数为，记作: 在此定义下的李括号为： 注意点：这里的李括号是推导出的，而不是定义的

与的为指数映射：

李代数

对应的李代数为,记作: 注意点：这里的指的是向量到矩阵的转换，不仅仅是反对称矩阵

在此定义下的李括号为：

指数与对数映射

上的指数映射

定义指数映射： 设，其中,于是有：

化简得： 可以看出指数映射即罗德里格斯公式

上的指数映射

其中：

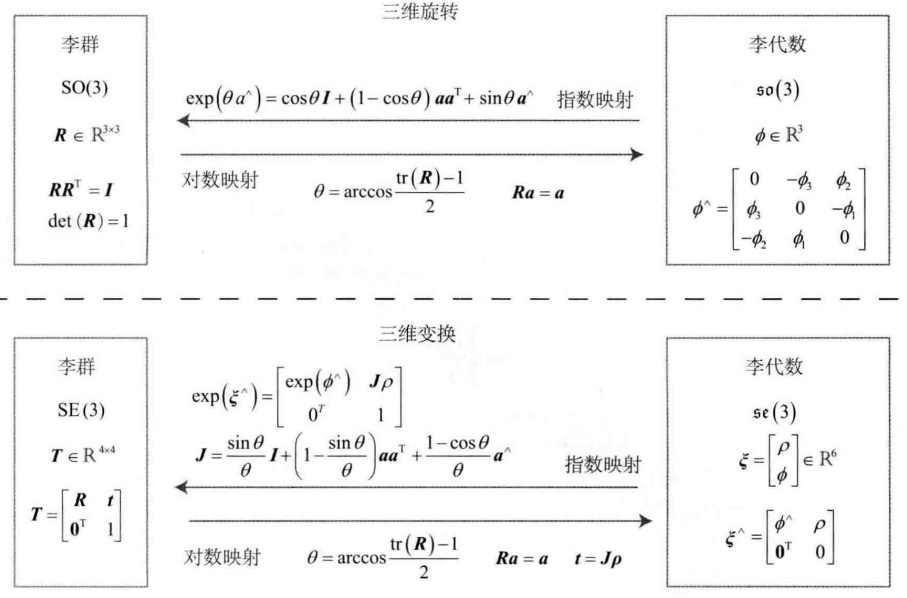
对应关系总结

李代数求导与扰动模型

公式与近似形式

公式： 上的近似表达： 其中：